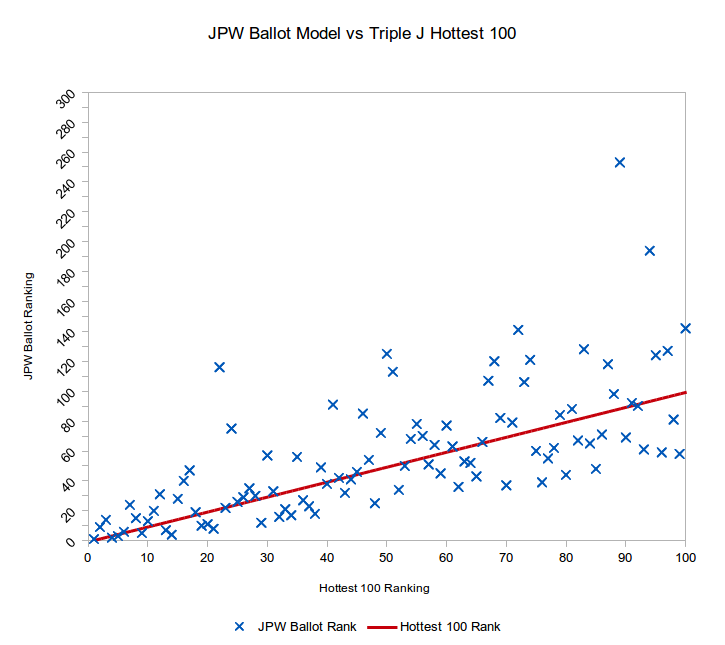
Now that we have the official results, let’s take a look at how we did! All models are wrong, some are useful.
Firstly, my model picked 85 songs as being in the top 100, so we missed 15. So did the Warmest 100 list. We got 4 exactly right, as did the Warmest 100. So far, they’re basically equivalent in that both models got a lot of them wrong. Let’s look at the degree of wrongness.
My first model was wildly inaccurate. It only found 62 of the top 100 songs, which is better than chance, but not by a lot. The average ranking error was a massive 197 places, mostly caused by songs with a couple of data points, but not many, getting ranks around 700 or so. Clearly that model needed refinement. If we use a log scale instead (abs(log(myrank)-log(officialrank)), which means larger errors at the tail end of the rankings don’t count as much, we get an average error of 1.957. We’ll use this value to compare accuracy with other models.
Let’s compare it to the more sophisticated ballot matching model: The average ranking error was only 22.4, much better! And on log scale, the average error is 1.6. Clearly, this model was a vastly better predictor than the original version.
Warmest 100 Model Performance
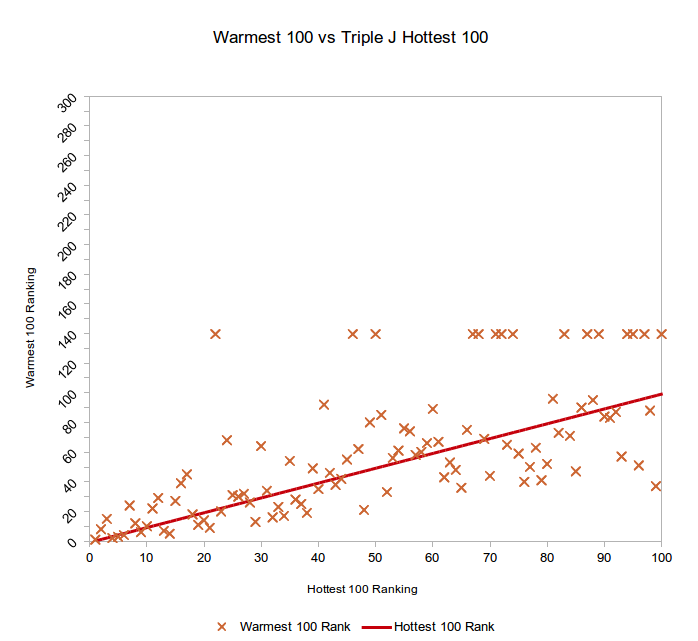 The Warmest 100 is a little tricky to assess, because I don’t have the full rank data, just the top 100 songs. This means I can’t account for the error of songs placed outside the top 100, so I can’t do a fair comparison with my models. If we set the rank of songs >100 to an arbitrary number, we can get an idea of the overall accuracy of the model.
The Warmest 100 is a little tricky to assess, because I don’t have the full rank data, just the top 100 songs. This means I can’t account for the error of songs placed outside the top 100, so I can’t do a fair comparison with my models. If we set the rank of songs >100 to an arbitrary number, we can get an idea of the overall accuracy of the model.
To start with, I set the rank to 0, so songs closer to 1 get marked with less error than they actually have, on average, so this is a kind assessment. The average rank error is 23.55 using this method, so not as good as my ballot model, but not by lots. To do the log ranking, we have to ignore these values (because log(0) is NaN) which again artificially improves the result. The log error average is thus 1.517, which is better than my ballot model.
If we instead set the ‘miss’ value to rank 100, we get different numbers: an average rank error of 16.25, and a log error of 1.590. Better on one, and worse on another. But that’s because there are more misses at higher ranks, which are closer to 100 than to 0, so that’s why the average rank error went down. Not really helpful, is it?
But let’s look at how wrong my misses were: the average rank of songs I ranked as > 100 was 139.47, so what if we set the Warmest 100 misses to the same value? This is like saying that the Warmest 100 is no better or worse than my model for songs ranked > 100, so this should be a more fair comparison.
That changes the average rank error for the Warmest 100 to 22.17, and the log error to 1.611, so slightly better than my ballot model, but not by much at all. However, if we go back to my ballot model and ignore the >100 rank values for the log error analysis, just as we did initially for the Warmest 100, the average log error is 1.506, which is better than the Warmest 100, but again, not by much.
Without access to the missing 15 values (15% of the total data set!) we can’t really distinguish between the two models. Either one might be slightly better than the other, we can’t be sure.
Improvements for Next Time
However, I know that my model ended up with 15,140 votes, and there are a bunch more that the model simply ignored. I could harvest more data by tuning the algorithm a bit, and either being more lenient about how ballots are counted, or by cleaning up the raw data so more ballots get counted. Either way should improve the results.
What we can’t fix is any underlying bias in the sample population: People who post their votes to Instagram are only partially representative of the overall Hottest 100 voting population. I have no idea if that’s a good or a bad thing.
What’s really interesting to me in all of this is how much data leaked out even though TripleJ didn’t provide an official way to share your votes this year. It highlights just how much information you can glean about something by using fairly rudimentary statistics on publicly shared data. And there is just so much data out there to look at, just sitting there in plain sight.
Imagine what people can do with all the data that isn’t in plain view.
You can look at the data in a spreadsheet in Google Docs if you’re so inclined.